Signal recently published a new, post-quantum secure, version of their X3DH protocol called PQXDH. As with any new cryptographic protocol, it is important to precisely analyse its security properties, especially for something as important as Signal.
In this blog post we give an overview of PQXDH and describe how we modeled its security using two formal verification tools (ProVerif and CryptoVerif). We detail some issues we found, and how we, a mix of Inria researchers, Cryspen researchers and Signal developers, worked together to improve the PQXDH specification.
First and most important: we did not find any serious issues in the design of the protocol. Nonetheless, there were a few imprecisions and potential pitfalls that the analysis pointed out:
- A potential public key encoding confusion attack between Diffie-Hellman keys and PQ KEM keys, which could theoretically break the security of PQXDH, and also (surprisingly) of X3DH. We verified that this attack was impossible to exploit in the current Signal implementation.
- A KEM re-encapsulation attack, even when considering IND-CCA secure KEMs, which implies that the compromise of a single responder’s
PQPKin fact compromises all its otherPQPK', even future ones. We verified that this is impossible when PQXDH is instantiated using Kyber as its KEM. - Some cryptographic assumptions that were not explicit in the specification (notably the security requirements on the AEAD) and the discussion of existing work in the Security Considerations section was slightly imprecise.
In response to these findings, Signal published a new version 2 of the specification and is considering some breaking changes for the next version of the protocol.
Over the new version 2 of the protocol, we were able to obtain the following positive results:
- Using the ProVerif symbolic analysis tool, we prove authentication and secrecy in the Dolev-Yao model, and enumerate the precise conditions under which the attacker can break these properties. Notably, we verify forward secrecy, resistance to store-now-decrypt-later quantum attacks, resistance to key compromise impersonation, and session independence.
- Using the CryptoVerif prover, we prove the computational secrecy and authentication of any completed key exchange under the GapDH assumption for the X25519 curve, the UF-CMA assumption on XEdDSA (assuming no key reuse between XEdDSA and X25519), the hash function modeled as a random oracle, and the IND-CPA+INT-CTXT assumptions for the AEAD.
- In CryptoVerif, we also show forward secrecy when the signature was UF-CMA secure at the time the key exchange took place, assuming post-quantum IND-CCA security for the KEM, modelling the hash function as a PRF, and IND-CPA+INT-CTXT security for the AEAD.
Notably, this is the first machine-checked post-quantum security proof of a real-world cryptographic protocol. We were able to obtain it thanks to the recent extension of CryptoVerif that supports post-quantum attackers [PQCV].
Quantum Resistance and the Signal Protocol (PQXDH)
You can find a high level description of the PQXDH protocol in Signal’s blog post and a detailed description of PQXDH in the protocol specification.
At a high level, the PQXDH protocol can be seen as injecting a post-quantum secure shared key into the classical X3DH protocol. The shared secret, output by the post-quantum KEM (CT, SS) = PQKEM-ENC(PQPK_B), is used in a key derivation function SK = KDF(DH1 || DH2 || DH3 || DH4 || SS) together with the four Diffie-Hellman values DH1 to DH4 from the X3DH.
Note that the fourth DH4 may be omitted if no curve one-time prekey OPK_B is present.
The following figure depicts the different keys used by the different parties.
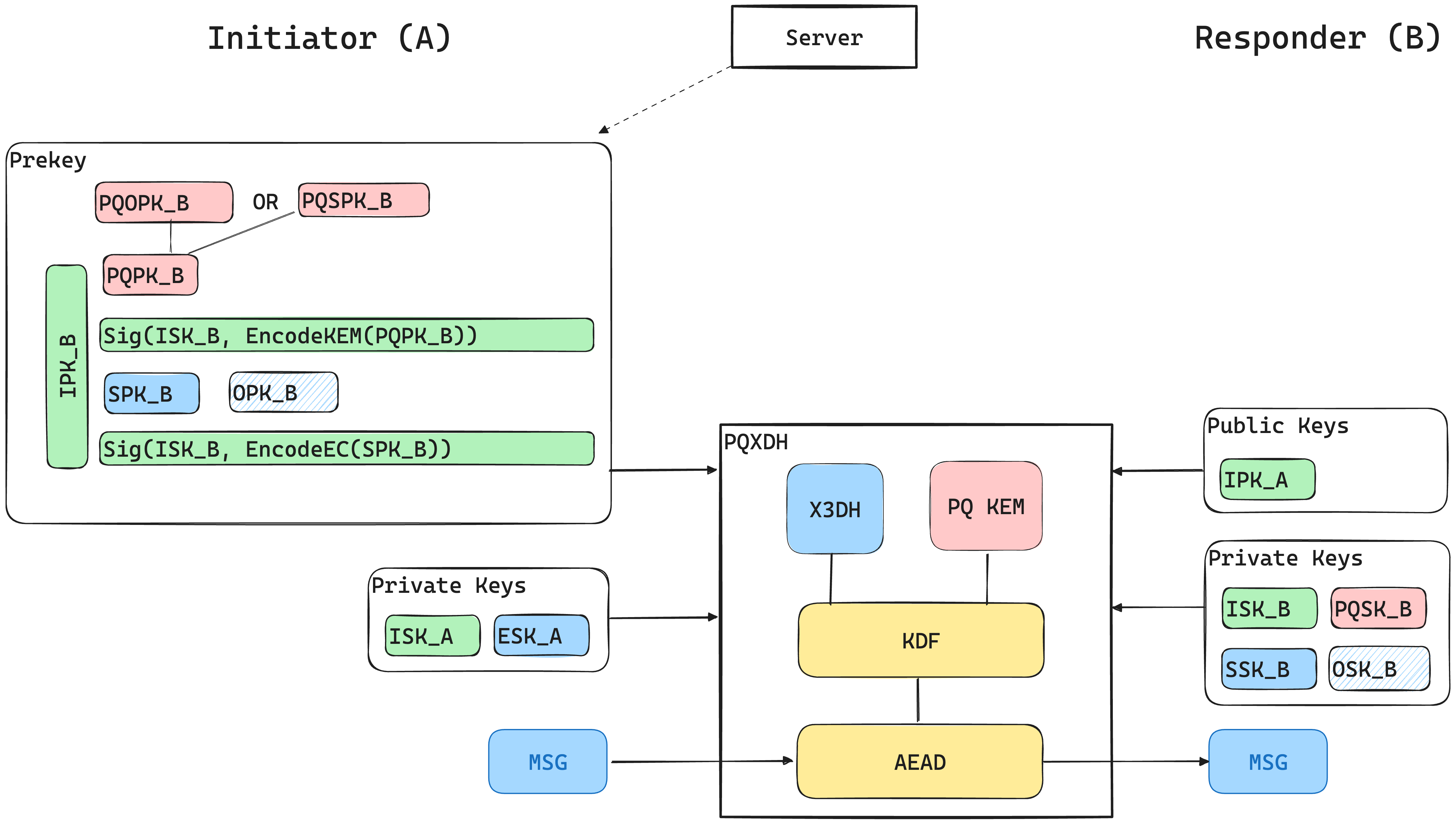
The initiator (A) retrieves the responder’s prekey bundle from the server, containing the responder’s (B) signed post-quantum public key (either a one-time key PQOPK_B or a last-resort key PQSPK_B), signed curve prekey SPK_B, and an optional one-time curve prekey OPK_B. A verifies the signatures using B’s identity public key IPK_B, generates an ephemeral curve key ESK_A, and feeds its private keys and all of B’s public keys to PQXDH, which generates with a key derivation based on several curve computations and an additional KEM computation an AEAD encryption key SK that is used to encrypt the first application message from A to B.
At the other end, upon receiving the encrypted PQXDH message, the responder B passes in its own private keys and A’s identity public key IPK_A to PQXDH, which proceeds to generate SK, verifies the incoming message, and decrypts the first application message from A.
Some Background on Formal Verification
Formal verification tools like ProVerif and CryptoVerif aim to provide strong security guarantees for cryptographic protocols by building machine-checkable security proofs.
ProVerif works in an abstract model of cryptography, sometimes called the symbolic or Dolev-Yao model, which treats cryptographic primitives as symbolic functions, abstracting away from the precise treatment of probabilities in cryptographic assumptions. ProVerif is very efficient and fully automated, and it allows users to quickly analyse protocols in many scenarios and search for potential attacks.
CryptoVerif formalises and partially automates classical cryptographic proof techniques, where we can obtain security under common cryptographic notions such as IND-CCA or UF-CMA. Thanks to a recent extension in [PQCV], CryptoVerif also allows us to analyse protocols against passive quantum attackers, which is especially valuable in a setting like PQXDH, where the protocol is designed to defend against store-now-decrypt-later attacks.
Formal Modeling
The first step in analysing the PQXDH mechanism is modelling it in ProVerif and CryptoVerif, together with the desired security properties. The models we wrote can be found on Github.
At a high level, the ProVerif and CryptoVerif models for PQXDH account for the following:
- an arbitrary number of client devices communicating with each other;
- each device uploads Curve and KEM keys to a server which is fully untrusted (modelled as a public channel);
- each connection consists of one message from the initiator to the responder (with no follow-up messages);
- the long-term Curve and KEM keys of certain devices may be compromised;
- the one-time Curve and KEM keys are never compromised;
- an attacker may suddenly be able to compute discrete logs (simulating the arrival of a powerful quantum computer), or be able to break all KEM encapsulation (capturing the possibility that a recently standardised KEM may not be as secure as we hope).
Security Properties
In both models, we want to prove the following security properties:
- Sender and message authentication
- (Forward) Secrecy of messages sent between uncompromised devices
- Forward secrecy even in the presence of a quantum attacker, as long as all KEM private keys remain uncompromised
- Resistance to KCI attacks (when using one-time keys)
- Resistance to identity misbinding attacks (when using a trusted PKI for identity keys)
We do not prove:
- Replay protection (since we do not model one-time key deletion)
- Any kind of deniability
Findings
In this section we describe the specific issues we found while modelling the protocol and trying to prove the previously stated properties.
Public Key Confusion Attack
The encoding functions are left a bit loose in the specification, so the model needs to make a choice. In our CryptoVerif model, we were forced to assume that EncodeEC and EncodeKEM have disjoint co-domains in order to complete the proof.
We do not model multiple curves and KEMs, but if we did, we would also
assume that EncodeEC for different curves has different results, and
similarly for EncodeKEM. These properties are crucial for security,
and without them we cannot prove unambiguity for the cryptographic
formats. A recent analysis of formats for several protocols
shows the general issues that arise from encoding collisions.
In ProVerif, we in fact did model that EncodeEC and EncodeKEM used ambiguous formats. ProVerif then gave us a potential attack on PQXDH that goes as follows:
- An attacker (acting as the untrusted server) sends an
SPKinstead of thePQPKto an initiator. - If the length of the KEM public keys and curve public keys are equal, the initiator would accept these keys and the PQXDH protocol would proceed.
- The initiator then tries to compute an encapsulation but using a curve element instead of a KEM public key.
- Since the security guarantees of the KEM only hold with honestly generated public keys, the shared secret is likely to be weak and guessable by the attacker.
A similar attack appears if the attacker sends the KEM public key PQPK in place of the curve public key SPK. Here, we in fact make 3 out of the 4 DH weak, and downgrade the security of even the classic X3DH.
In both cases, the attacker has used one crypto construction (KEM or DH) to attack the other because of an encoding ambiguity.
Interestingly, this issue illustrates how adding an extra, provably-secure component to an already-secure protocol may in fact downgrade the guarantees of the protocol. This serves as a cautionary tale for other protocols seeking to use hybrid constructions for post-quantum security.
In the Signal implementation, this attack is prevented, since the key sizes of Kyber and X25519 cannot match, and in addition each key is prefixed by a byte identifying the algorithm. Yet, adding format disjointness as an explicit condition to the specification prevents any future problems with other KEM/DH combinations, or for other independent implementations.
Weak Post-Quantum Forward Secrecy
The post-quantum forward secrecy guarantee of PQXDH relies on the initiator using a signed one-time KEM public key PQOPK and the responder deleting the corresponding private key after receiving the PQXDH message. However, since both the PQOPK and the signed last-resort KEM key PQSPK are signed with the same key, and both have the same encoded format, it is impossible for an initiator to know whether they are using a last resort or one-time key.
As a consequence, PQXDH offers a weaker forward secrecy guarantee than the initiator may expect, since the initiator cannot know if the decryption key will be immediately deleted. In practice, however, the last-resort key PQSPK is a medium-term secret, and will be deleted by the responder after some time.
Still, it is easy to fix the specification and provide a stronger forward secrecy guarantee, simply by using disjoint formats within the signatures of the signed one-time and last-resort keys.
KDF Input Confusion Attack
At first glance, it may appear that PQXDH also has an encoding ambiguity in the format of keys used in various calls to the key derivation function (KDF) in the protocol. In fact, the info field contains enough information though to disambiguate these KDF calls.
In our first ProVerif model, we ignored the info field and the tool found several cross-protocol attacks. Ignoring such seeming low-level details when modeling a protocol can sometimes miss attacks, and at other times find false attacks.
Even after accounting for the info field, there remains a concern that the format of the KDF input key material between X3DH and PQXDH can be confused with each other. For example, X3DH may use 3 or 4 DH shared secrets concatenated with each other as the KDF input, while PQXDH concatenates either 3 DH and 1 KEM secret, or 4 DH and 1 KEM secret. Within PQXDH, the info field prevents confusions, but there could still theoretically be a cross-protocol attack between PQXDH (3DH+SS) and X3DH (4DH) depending on what info field the application chooses in X3DH, since the X3DH specification does not mandate the contents of its info fields.
This is another interesting instance where the composition of two protocols can potentially result in attacks even if both protocols are individually secure.
KEM Re-Encapsulation Attack
We show that when using an IND-CCA secure public key encryption scheme to build an IND-CCA secure KEM, an attacker can make two parties compute the same key, even though both used a distinct PQPK, as soon as only one of the PQPK was compromised.
This attack is a new attack in the class of re-encapsulation attacks as introduced by Cremers, Dax, and Medinger.
Consider the following execution:
- An attacker is able to compromise some
PQPKof responder B, while anotherPQPK2of the same responder is uncompromised. - The attacker makes initiator A use
PQPK, and obtain a ciphertextCT, from which it can learn the shared secretSS, asPQPKwas compromised. - Now, the attacker, not violating IND-CCA, comes up with a new ciphertext
CT', valid forPQPK2, such that the decapsulation ofCT'is alsoSS. - The attacker then forwards to B the message from
A, but swapsCTbyCT', and the key identifier ofPQPKbyPQPK2. - The responder B succeeds in computing the key using
PQPK2.
The main issue here is that the compromise of a single PQPK in fact enables an attacker to compromise all future KEM shared secrets of the responder, and this even after the responder deleted the compromised PQPK.
As this attack can be carried out without violating the IND-CCA assumption, it turns out that the IND-CCA security of the KEM scheme is not enough to show the full security of PQXDH. We in fact require an additional assumption, which is not a classical cryptographic one, but which informally captures that the shared secret is strongly linked to the public key.
While many schemes such as Kyber/ML-KEM do include the public key in the shared secret derivation, it may be prudent to add PQPK somewhere else in the protocol, for instance in the associated data of the AEAD encrypted message or directly in the KDF. Such changes are considered for a next version of the PQXDH protocol.
This is an important observation, as some KEM designers explicitly state that “Application designers are encouraged to assume solely the standard IND-CCA2 property” [MCR], and notably, both HQC and BIKE do not directly tie the shared secret to the public key, but only to the ciphertext.
Additional Insights
While modeling the protocol, we also found a few places where the protocol description was not precise enough. These are not necessarily shortcomings in the protocol, but under-specifications.
PQXDH (like X3DH) uses the same Diffie-Hellman keypair for both X25519 curve computations and XEdDSA signatures. No precise security assumption for this key re-use exists (see Thormarker21 for a discussion on similar issues). We make a simplifying assumption in the CryptoVerif model, where the identity key is split into two separate keys, one used for X25519 computations and the other for XEdDSA signatures.
The PQXDH protocol does not explicitly model the AEAD that is used with the session key SK generated in the protocol. It does not specify, for example, how the AEAD nonces are derived. In our models, we assumed that the nonce is a constant (zeroes). We did not model any response messages from responders to initiators, but if we did, we would be able to detect vulnerabilities such as nonce re-use. In the CryptoVerif model, we require IND-CPA and INT-CTXT security of the AEAD scheme in order to prove security.
Protocol Updates and Security Theorems
Based on our findings above, we worked with the Signal protocol designers on addressing all the issues we found in the protocol specification. In the updated specification document:
- The description of the parameters now includes the security properties of the PQ KEM scheme (IND-CCA), the AEAD (IND-CPA and INT-CTXT), and the disjointness of the encoding functions.
- The protocol specification now emphasises that the clients should be able to identify whether a PQ KEM key is the last-resort or an ephemeral key.
- The specification now requires that
PQPK_Bis added to the additional dataADof the AEAD if it is not used internaly in the KEM to derive the shared secret. Combined, this prevents the KEM re-encapsulation issues described above.
We modeled all these changes in our ProVerif and CryptoVerif models and were able to prove all the desired security properties of the protocol, hence establishing machine-checked symbolic and computational security theorems for PQXDH.
Like all formal analyses, our theorems also have limitations. The results only hold for our models of PQXDH, which may (and do) miss some low-level details of the protocol implementation. For example, we assume that the protocol uses different identity keys for signatures and Diffie-Hellman, which is not true in practice.
The ProVerif results only hold in the symbolic model, but consider a wide range of compromise scenarios, and should be seen as providing confidence against a large class of logical protocol vulnerabilities. Conversely, the CryptoVerif model amounts to a full cryptographic proof based on precise computational assumptions, but it does not capture all possible combinations of compromises, in order to bound proof complexity.
Despite these limitations, we find it remarkable that these tools enabled us to produce machine-checked proofs for a real-world protocol within a month of its publication. By sharing these models and working on them together with experts from Signal, we were able to quickly validate various proposed changes to the specification. This bodes well for the applicability and effectiveness of formal verification tools for new post-quantum protocol designs.
Acknowledgements
This analysis is joint work between INRIA, Cryspen and Signal. It was inspired by a previous CryptoVerif model for TextSecure (a variant of X3DH) made by Bruno Blanchet. Théophile Wallez gave precious insights about the potentially ambiguous encodings used in the specification.
References
- Our analysis : https://github.com/Inria-Prosecco/pqxdh-analysis
- PQXDH specification: https://signal.org/docs/specifications/pqxdh/
- PQCV: CryptoVerif: a Computationally-Sound Security Protocol Verifier, Bruno Blanchet and Charlie Jacomme. Inria Research report RR-9526. Oct 2023.
Get in touch